Header image by Cryptography is the cornerstone of modern digital security. From encrypted messaging to blockchain and secure web browsing, the invisible machinery of math keeps our data safe. But with the rise of quantum computing, the very foundation of today's encryption methods faces a serious threat.
Let's explore what cryptography is, how it works, and why quantum computers could break it — unless we prepare now.
What Is Cryptography?
Cryptography is the art of protecting information through mathematical transformations. It ensures that only the intended recipient can access a message's contents, even if others intercept it.
There are two major types of cryptography:
- Symmetric cryptography: The same key is used to both encrypt and decrypt the message.
- Asymmetric cryptography: Uses a pair of keys — one public, one private.
Cryptography underpins much more than hidden messages. It enables secure communications, digital signatures, and the backbone of technologies like blockchain, e-commerce, and VPNs.
A Classic Example: Caesar Cipher
One of the simplest and oldest encryption techniques is the Caesar cipher.
Each letter in a message is shifted by a fixed number of positions in the alphabet. For example, with a key k = 3:
$$\texttt{A} \rightarrow \texttt{D}, \quad \texttt{B} \rightarrow \texttt{E}, \quad \texttt{C} \rightarrow \texttt{F}, \quad \ldots$$
So the message ATTACK becomes DWWDFN.
Today, this cipher is trivially breakable — one only needs to try all 26 k possibilities. However, it still serves as a useful introduction to basic encryption concepts such as:
- Cipher key, in this case k = 3;
- Plaintext and ciphertext, ATTACK and DWWDFN respectively.
Diffie-Hellman
While the Caesar cipher illustrates the basics of encryption, it lacks the security needed for real-world communication. Modern systems require a way for two people to establish a shared secret key — even when communicating over an insecure channel.
This raises an important question:
How can two people agree on a secret if everyone can hear their conversation?
This is the problem that Diffie-Hellman key exchange solves. It allows two parties to create a shared secret, without ever sending the secret itself.
Historically, the Diffie-Hellman key exchange is credited to Whitfield Diffie and Martin Hellman, who published it in 1976. However, Ralph Merkle also contributed key ideas, and Diffie has since acknowledged him as a co-inventor.
But, to explain how this works, start with a simple analogy using colors.
- Imagine Alice and Bob want to exchange a secret.
- Alice chooses a secret color: red.
- Bob chooses a different secret color: blue.
- They agree on a public base color: gray.
- Each mixes their secret color with the public one and sends the result:
- Alice sends a mixture of red + gray
- Bob sends a mixture of blue + gray
- Then, each mixes the received color with their own secret:
- Alice mixes (blue + gray) with red
- Bob mixes (red + gray) with blue
- The final result is the same shared color — a shared secret key — but anyone observing the exchanged colors can’t reconstruct it without knowing the secrets.
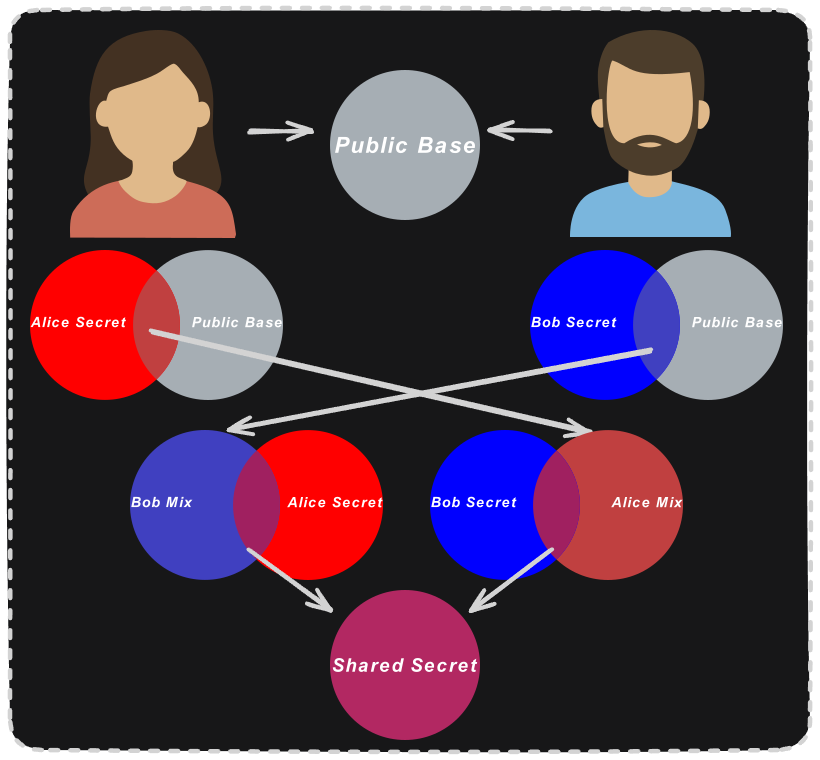Diffie-Hellman as Colors Scheme by gabrielzschmitz, licensed under Creative Commons 4.0 Attribution license.
Turning Colors into Numbers
We'll now translate the color analogy into mathematical operations — this is where the real magic of Diffie-Hellman happens.
In the previous example, Alice and Bob created a shared color without ever revealing their secret colors. The same principle can be achieved with numbers using modular arithmetic, which is like working on a circular number line — much like a clock.
For example:
$$10 + 5 \equiv 3 \pmod{12}$$
This “modulo” operator keeps values within a fixed range, which prevents attackers from deducing secrets even when partial information is shared.
How the Protocol Works
-
Public parameters are agreed upon:
- A base number
g(generator) - A large prime number
p(modulus)
- A base number
-
Alice and Bob choose private numbers:
- Alice chooses a secret number
a - Bob chooses a secret number
b
- Alice chooses a secret number
-
They generate public values using modular exponentiation:
$$A = g^a \pmod{p}$$
$$B = g^b \pmod{p}$$
They exchange
AandBover an open channel.They each compute the same secret key:
$$\text{Alice: } K = B^a \pmod p = g^{ba} \pmod p$$
$$\text{Bob: } K = A^b \pmod p = g^{ab} \pmod p$$
as:
$$g^{ab} = g^{ba}$$
Both parties arrive at the same shared key — just like the shared color in the metaphor — even though their private values remain hidden.
Security Through Discrete Logarithms
Now that we've seen how Alice and Bob generate a shared secret, let's explore why an attacker can't just reverse the process.
Even though the values g, p, A, and B are publicly visible, the attacker still doesn't know the private values a or b.
Why can't they just compute them?
Because doing so would require solving the discrete logarithm problem — finding a such that:
$$A = g^a \pmod{p}$$
This problem is computationally hard for large enough values of p. There's no efficient shortcut to reverse modular exponentiation without knowing the secret exponent. In fact:
- For modern key sizes, it would take longer than the age of the universe using today's best classical algorithms.
"Or would it?"
This is the tipping point where classical security assumptions fall apart.
Enter quantum computing.
The Quantum Problem
Quantum computers can solve discrete logarithms exponentially faster than classical ones using Shor's Algorithm.
That means encryption schemes like RSA, Diffie-Hellman, and ECC — the bedrock of internet security — could be broken in minutes by a powerful quantum machine.
Large-scale quantum computers don't yet exist. But when they arrive, most of our current cryptographic infrastructure will become obsolete.
Why We Need Post-Quantum Cryptography
Post-Quantum Cryptography (PQC) is about building encryption systems that resist attacks from quantum computers.
Instead of relying on problems like factoring or discrete logs, PQC is based on:
- Lattices
- Hash-based constructions
- Multivariate polynomials
- Code-based systems
These problems remain hard even for quantum machines.
Institutions like NIST are already evaluating and standardizing PQC algorithms to ensure future-proof digital security.
Conclusion
Cryptography has come a long way — from Caesar’s ciphers to internet-scale encryption. But a new challenge looms: the quantum computer.
If we want to preserve privacy, trust, and security in the digital age, we must act now to transition to post-quantum cryptography.
The future isn't just encrypted. It's quantum-resistant.
Further Reading
-
Palomar College (2018) "Basic and Historical Cryptography" slide set. Introduces Caesar cipher as E(p,k) = (p + k) (mod 26). 📄 Slide Deck PDF
-
Whitfield Diffie & Martin E. Hellman (1976) "New Directions in Cryptography," IEEE Trans. Inf. Theory 22(6): 644–654. Seminal paper introducing public‐key cryptography and digital signatures. 📄 Read PDF from Stanford
-
Rivest, R. L., A. Shamir & L. Adleman (1978) "A Method for Obtaining Digital Signatures and Public-Key Cryptosystems," Commun. ACM 21(2): 120–126. Introduces the RSA algorithm and shows how to enable secure communication without prior key sharing. 📄 Read PDF from MIT
-
Peter W. Shor (1994) "Polynomial-Time Algorithms for Prime Factorization and Discrete Logarithms on a Quantum Computer." Shows that a quantum computer can break RSA and Diffie–Hellman by factoring and computing discrete logs in polynomial time. 📄 Read on arXiv (quant-ph/9508027)
-
Leslie Lamport (1979) "Constructing Digital Signatures from a One-Way Function." First one-time signature scheme based on hash functions — a precursor to hash-based cryptography. 📄 SRI Technical Report (CSL-98)
-
Oded Regev (2005) "On Lattices, Learning with Errors, Random Linear Codes, and Cryptography," in Proc. 37th ACM STOC. Introduces the Learning With Errors (LWE) problem and a quantum-resistant public-key encryption scheme. 📄 Read PDF from STOC (2005)
-
Dam, D.-T. et al. (2023) "A Survey of Post-Quantum Cryptography: Start of a New Race," Cryptography 2023, 7(3): 40. An accessible and up-to-date survey of PQC approaches, NIST candidates, and research directions. 📄 Open-access MDPI paper
You can read the original blog post at: gabrielzschmitz.github.io
OpenArt AI-Generated "Pitfalls and holes in Cryptography using a dark theme", except for the 
